Finalmente hemos llegado... Ebenezer..! Solo resta un pequeño esfuerzo adicional chicos. Ese esfuerzo significará concentrarnos y enfocarnos esta semana que viene en resolver y repasar estos problemas que te presento en esta práctica, que es el Repaso General del Cuatrimestre.
Temas como: Porcentaje y conversión
a fracción y decimal, aplicación de porcentajes en problemas de descuentos,
incrementos, diezmos, impuestos, etc.; método de la Regla de Tres para solución
de problemas, Sistema Métrico Decimal, la identificación de sus prefijos y
movimientos entre los múltiplos y submúltiplos de la escala, Sistema Inglés,
equivalencias, conversiones simples, conversiones complejas, reglas de oro para
conversiones entre Sistemas de Unidades, Geometría enfocada en conceptos de área en unidades cuadradas
(m²), calculo de área de un cuadrado, de un rectángulo, de un triángulo, de una
circunferencia; así como volumen en unidades cúbicas (m³), cálculo de volumen de una caja, de una
piscina, de una pirámide, de un cilindro, de un cono, o el cálculo de otras
dimensiones del poliedro dado su volumen sustituyendo variables en las
fórmulas, conceptos de ángulos y sus diferentes clasificaciones, medición de
ángulos, polígonos, triángulos y su clasificación por sus ángulos interiores y
por la longitud de sus lados, y finalmente Estadísticas y organización/tabulación de datos,
representación en gráfica de frecuencias e hitos estadísticos, todos los cuales te los he mencionado en orden cronológico para mayor facilidad al recordarlos, los verás en esta práctica que trataré de explicarte y resolver uno o dos de sus problemas.
Tu debes resolver el resto...
I.- Completa la tabla con sus respectivos porcientos,
fracciones y decimales equivalentes
Fracción
|
Decimal
|
Porciento
|
Para llevar una expresión porcentual a fracción solo debemos dejar representada su división entre 100; es decir, no solucionar la división hasta obtener el decimal, sino dejarla representada:
y esa es la fracción en sí misma. Si se puede simplificar, debemos proceder a hacerlo: en este caso, si arriba dividimos entre 5, también dividimos el denominador entre 5, y tendremos:
Al final, esta es la fracción equivalente a 45% y a 0.45.
|
Para convertir de porciento a decimal, lo único que debemos hacer es dividir la cantidad del % entre 100, por cuanto la misma representa una porción del todo, que es justamente 100:
45 ÷ 100 = 0.45
Realmente, esto no es otra cosa que correr el punto decimal hacia la izquierda dos veces, por cuanto el 100 tiene dos ceros.
|
45%
|
Convertir a decimal desde una fracción no es otra cosa que dividir el numerador entre el denominador:
1 ÷ 2 = 0.5
|
Convertir a expresión porcentual desde un decimal no es otra cosa que mover el punto hacia la derecha dos veces, por cuanto el 100 tiene dos ceros:
50%
|
|
Para convertir de un decimal directamente hacia una fracción, sin contar con la expresión porcentual, simplemente corremos el punto decimal tantas veces hacia la derecha como sea necesario para sacarlo del número, y dividimos por una potencia de 10 que contenga tantos ceros como veces hemos corrido el punto. Si corremos el punto 1 vez, dividimos entre 10 (tiene un solo cero). Si corremos el punto 2 veces, dividimos entre 100 (tiene dos ceros). Si corremos el punto tres veces, dividimos entre 1000 (tiene tres ceros), etc. La fracción de este problema es:
simplificando (dividiendo ambos el numerador y el denominador entre 2) tenemos:
|
0.06
|
|
0.86
|
||
30%
|
Ahora busca papel y lápiz porque el resto, como entenderás, debo dejártelos a ti...
II.- Con las gráficas siguientes escribe la fracción
que representa, el decimal que corresponde a esa fracción, y el porcentaje.
Entenderás que para estos ejercicios a continuación no te explicaré nada adicional, pues se trata de los mismos problemas anteriores. Asi que.... adelante..!
III.- Resuelve los siguientes problemas de
aplicaciones de porcentajes
Ahora los problemas de aplicación..! Pero no hay necesidad de asustarse, porque si partes de los principios que hemos repetido muchas veces en clase, podrás resolverlos sin mayores dificultades. Estos son los principios: siempre hay un todo en el planteamiento, y debes buscar la porción que se te pide (que es el porcentaje); o siempre hay una porción y deberás buscar el todo del cual esa porción dada es el porcentaje. Sencillo. A veces, te darán ambos el todo y la porción, y te pedirán el porcentaje que esa parte menor representa del monto o cantidad total.
Para remate, para estos casos siempre tomarás en cuenta una expresión numérica fija, que te ayudará a construir la regla de tres. Cuál es esa expresión? el número 100 en porciento; o sea, 100%.
Y para doble-remate, siempre tomarás en cuenta colocar % debajo de %, $ debajo de $, manzanas debajo de manzanas, etc. Mira el siguiente ejercicio:
A)
El dueño de una tienda de artículos para turistas
compra una vasija de barro a un artesano a $25, y le gana 75% ¿Cuánto dinero le
gana?
Si me dan el precio de la vasija y me preguntan por un porcentaje de ese precio, entonces ese precio que me dan es el todo; es decir, es el 100% para este caso. O sea, estamos frente a un problema donde me dan el todo, y me piden una porción de ese todo. Construiremos la regla de tres así:
eso se lee así: $25 es el 100%, y $x será el 75% de esos 25$. Cuidando de colocar, como dijimos antes, % debajo de %, $ debajo de $, etc. Entonces multiplicamos
en cruz y dividimos entre aquel número que no tiene pareja para
multiplicar. En este caso:
Tendríamos:
Entonces, $18.75 es la cantidad de dinero que se gana. En otras palabras, esa cantidad de dinero es el 75% de $25.
B)
Un tanque de gasolina tiene una capacidad de 45
galones. Otro tanque más pequeño puede
contener 25% de esa capacidad. ¿Cuál es la capacidad del nuevo tanque?
Por ejemplo, en este caso... ¿nos dan el todo y nos piden una porción, o nos dan una porción y nos piden el todo? Evidentemente nos dan 45 galones como el todo, y nos piden que digamos cuánto es la capacidad de otro tanque que puede almacenar 25% de la capacidad del primer tanque mas grande. Es decir, nos piden una porción del todo. Quedará así:
Luego:
Luego:
Entonces, 11.25 es la cantidad de galones que puede contener el tanque mas pequeño. En otras palabras, esa cantidad de galones es el 25% de 45gal.
C)
Supongamos que la sección de Básica del CBC tiene 400
alumnos, y que han ido de viaje a una excursión general 250 alumnos. ¿Qué
porcentaje de alumnos ha ido de viaje?
Tu solo...
D)
Una moto cuyo precio era de $5,000, cuesta en
la actualidad $250 más. ¿Cuál es el porcentaje de aumento?
Fíjate lo que te estan pidiendo aquí: cuál es el porcentaje..! Es decir, te dan montos en dinero, y te piden que calcules cuánto porcentaje es la porción de dinero (el cual es un monto que te indican) con relación al todo (que también es un monto que te indican). mmm... interesante...
Si tenemos un monto total (el todo), sabemos que ese es el 100%, no? Entonces escribimos:
Así:
Si tenemos un monto total (el todo), sabemos que ese es el 100%, no? Entonces escribimos:
y si tenemos una porción de dinero que nos dan, indicándonos que ese monto es la porción adicional que está por encima del precio original de la moto, podemos decir que ese dinero representa un porcentaje del monto original. Bueno, pues precisamente lo que nos estan preguntando es ese porcentaje; o sea, cuánto porcentaje (%) del monto original representan esos $250 de más en los cuales se vende hoy la moto. Entonces, por cuanto nos estan preguntando el porcentaje, colocamos la "x" debajo de porcentaje:
Entonces escribimos:Así:
E)
Al adquirir un vehículo cuyo precio es de $8,800, nos
hacen un descuento del 7.5%. ¿Cuánto dinero hay que pagar por el
vehículo?
Haz este. Fíjate que al final tienes que hacer un cálculo, no solo encontrar el porcentaje. Piensa... recuerda a que nos referimos cuándo hablamos de "descuento"... vamos, tu puedes...
IV.- Escribe las siglas de los múltiplos y
sub-múltiplos que faltan en la siguiente escala del Sistema Métrico Decimal:
V.- Escribe los nombres de las siglas que faltan en el problema anterior:
V.- Escribe los nombres de las siglas que faltan en el problema anterior:
_______________________________
_______________________________
_______________________________
_______________________________
_______________________________
_______________________________
_______________________________
_______________________________
_______________________________
VI.- Resuelve las siguientes conversiones de unidades
Aquí hemos indicado un procedimiento claro y sencillo:
1.- Dibujar la escala métrica con sus unidades correspondientes.
2.- Colocarnos en la unidad de la cual conocemos el valor.
3.- Movernos hacia la unidad que nos preguntan.
1.- Dibujar la escala métrica con sus unidades correspondientes.
2.- Colocarnos en la unidad de la cual conocemos el valor.
3.- Movernos hacia la unidad que nos preguntan.
4.- Considerar la cantidad de saltos (o curvitas) que podemos dibujar en la escala hasta llegar a la unidad deseada.
5.- Escribir la cantidad original tal como nos la dan.
6.- Mover el punto decimal tantas veces como saltos haya dibujado en la escala métrica.
7.- Rellenar con ceros los huecos que no contengan cifras.
Con lo anterior te será suficiente. Sigue esos pasos cuidadosamente, y lograrás la respuesta...
1.
Cuántos centímetros hay en 1.5 Hm?
2.
Cuántos milímetros hay en 20 dm?
3.
Cuántos Kilómetros están representados en 350
centímetros?
4.
Cuántos metros hay en 0.35Km?
5.
Cuántos Hectómetros hay en 1,897m?
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
VII.- Resuelve los siguientes problemas de aplicación
de conversión de unidades:
En estos problemas no se trata de nada más que de leer super-bien el planteamiento y tomar en cuenta un principio: convertir hacia la unidad en la que está dada la pregunta:
1.
La distancia entre la playa y mi casa es de 58Km. Si decido ir caminando la mitad del camino,
¿cuántos metros habré recorrido a pie?
Por ejemplo, aquí debemos convertir de Km a m, pero debes leer bien, bien, bien... porque fíjate que dice "Si decido ir caminando LA MITAD del camino". O sea, que solo convertiremos la mitad de esa distancia a metros.
De aquí en adelante está de más que te diga cómo hacerlo, pues es super-fácil, y ya lo hicimos en el punto anterior.
De aquí en adelante está de más que te diga cómo hacerlo, pues es super-fácil, y ya lo hicimos en el punto anterior.
2.
Tony preparó 14 L de limonada para una fiesta. Sus invitados se tomaron 9,500 ml de la
limonada. ¿Cuántos mililitros de limonada le sobraron a Tony?
Mira aquí, por ejemplo... la pregunta la hacen en mililitros (ml), entonces es preferible convertir esos 14L en ml. Luego que haga eso, podré calcular cuántos ml quedan si sus invitados se tomaron 9,500ml... sencillo: una resta. Entiendes?
3.
La iglesia de un pequeño pueblo está localizada a
3.5Km de distancia del parque central, y el pastor de esa iglesia vive a 500m
del parque en dirección a la iglesia.
Entonces, cuantos metros (m) debe recorrer el pastor cada Domingo desde
su casa hasta la iglesia?
4. En una cubeta vertimos 4.5 galones de agua y 1 litro de Mistolín.
¿Cuántos litros de líquido en total tendremos en la cubeta? Nota: 1gal = 3.8
litros (aprox.)
5. Cuántos ml tendremos en la cubeta del problema anterior?
VIII.- Calcula el volumen de los cuerpos indicados a
continuación:
Bueno, no creo que hayamos visto nada más fácil que esto: aplicación de fórmula para calcular el volúmen de un cuerpo... verdad? Si conozco el área del piso (o base) y conozco la altura del cuerpo, ya tengo el volumen. La fórmula es:
Claro... a veces no me dan el área del piso, sino que tengo que calcularla. Para calcularla debo utilizar las fórmulas conocidas de área de un cuadrado o un rectángulo, área de un triángulo, área de un círculo, etc. (bueno, en realidad solo hemos visto estos tres... en 7mo verás otros polígonos).
Recuerda que la fórmula cambia un poco cuando se trata de una pirámide o un cono:
ves el cambio? simple: se divide entre 3 cuando se trata de una pirámide o un cono.
1. Calcula el volumen, en metros cúbicos, de una habitación que tiene 5m de
largo, 4m de ancho y 2.5m de alto.
2. Una piscina tiene 8m de largo, 6m de ancho y 1.5m de profundidad. ¿Cuál
es su capacidad total en m3?
3. En un almacén de dimensiones 50m de largo, 30m de ancho y 20m de alto
queremos almacenar cajas de dimensiones 10m de largo, 6m de ancho y 4m de alto.
¿Cuántas cajas podremos almacenar? [Recuerda que se trata de distribuir el volumen
o capacidad total del almacén entre
el volumen que ocupan las cajas]
Orejita: calcula ambos volúmenes por separado: el del almacén, y el que ocupan las cajas. Luego, fíjate bien lo que dice la nota en rojo para que concluyas el problema.
4. El área del piso de un edificio mide 50m2 y su altura es de
20 pisos. Si cada piso mide 3m de
altura, ¿cuánto será la capacidad total del edificio?
Este es mas simple que el anterior, solo se trata de pensar un poco: si has podido calcular el volumen de un (1) piso, y el problema te dice que el edificio tiene 20 pisos... ¿qué tienes que hacer?
5. Calcula el volumen de estos cuerpos:
6.
Si las figuras del problema anterior fuesen pirámides
con las mismas bases y con la misma altura, ¿cuál sería su volumen?
7.
Calcula el volumen de un prisma cuya base es
rectangular y tiene un lado de 8cm y otro de 5cm. La altura del prisma es de
10cm.
IX.- Calcula el volumen o cualquier otra dimensión que se te pida sobre los cuerpos indicados a continuación:
IX.- Calcula el volumen o cualquier otra dimensión que se te pida sobre los cuerpos indicados a continuación:
En estos tipos de problemas estamos hablando del mismo concepto: aplicación de fórmulas. Solo que las fórmulas se consiguen derivando las variables (o letras) deseadas a partir de las fórmulas conocidas. Por ejemplo, si me piden "h" (altura de un cuerpo), y me dan su volumen y el área de su base (o piso), primero debo encontrar la fórmula a utilizar. Para esto debo tomar en cuenta:
a.- Dejar sola la variable o letra que estoy buscando.
b.- Toda otra variable o letra se debe mudar para el otro lado del sigo de igual (=). Es como si vivieran en una casita de un lado del signo, y deben mudarse para una casita al otro lado del signo; solo que cuando se mudan, pasan a realizar la operación contraria a la que hacían antes. Si antes sumaban, pasan restando. Si antes multiplicaban, pasan dividiendo, y asi....
a.- Dejar sola la variable o letra que estoy buscando.
b.- Toda otra variable o letra se debe mudar para el otro lado del sigo de igual (=). Es como si vivieran en una casita de un lado del signo, y deben mudarse para una casita al otro lado del signo; solo que cuando se mudan, pasan a realizar la operación contraria a la que hacían antes. Si antes sumaban, pasan restando. Si antes multiplicaban, pasan dividiendo, y asi....
1. ¿Cuál es el volumen de una pirámide con base triangular de lados igual a
9.5 cm y una altura de 8cm? La altura de la pirámide es 16cm
2. ¿Cuál es el volumen de un cono cuya base tiene un radio que mide 3m. La altura del cono es de 15m
3. ¿Cuál será la altura de un prisma cuyo piso tiene un área de 830cm2 y su volumen es de 2400cm3?
Por ejemplo: me piden la altura (h), entonces, si la fórmula de volumen es:
la fórmula de altura será:
porque hemos dejado sola a la "h", y hemos pasado "Ab" dividiendo porque antes estaba multiplicando. Ahora, solo se trata de sustituir los valores y proceder con la operación.
4. Se nos informa que una pirámide tiene una altura de 24.8cm. y un volumen de 5400cm3 y ¿Cuánto es el área de la base?
la fórmula de altura será:
porque hemos dejado sola a la "h", y hemos pasado "Ab" dividiendo porque antes estaba multiplicando. Ahora, solo se trata de sustituir los valores y proceder con la operación.
4. Se nos informa que una pirámide tiene una altura de 24.8cm. y un volumen de 5400cm3 y ¿Cuánto es el área de la base?
Aquí me piden el área de la base, pero fíjate con cuidado que se trata de una pirámide. Intenta despejar "Ab" sabiendo que se trata de la fórmula:
5. Calcular el volumen de un cilindro que mide 3pie de altura, y su base es
un círculo con 2pies de radio.
X.- Define:
Recta: _____________________________________________________________________
Segmentos de Rectas:
______________________________________________________
Paralelismo:
_________________________________________________________________
Perpendicularidad: _________________________________________________________
XI.- Dibuja e indica con la nomenclatura adecuada:
XII.- Con los siguientes datos, construye una tabla de puntos y haya el Mínimo, Máximo, Rango, Moda, Mediana y utilizando tu calculadora, encuentra la Media (Promedio):
Datos Crudos que corresponden a la votación del presidente de la comisión
estudiantil de Básica del CBC:
1.- Construir la recta de la Gráfica de Frecuencia.
2.- Cuidar de construirla desde el menor de los valores crudos hasta el mayor de ellos.
3.- Ir anotando cada ocurrencia, sin olvidar ir tachandolos en la lista cruda para evitar perder el orden.
4.- Construir la Tabla de Frecuencia, anotando cada valor y anotando a su lado la cantidad de veces que se repite.
5.- Hallar los Hitos Estadísticos: MIN, MAX, RAN, MOD, MED y PROM.
Recuerda que para la MEDiana debemos listar en una linea cada valor en orden de menor a mayor, repetidos tantas veces como indique la Tabla de Frecuencia. Si esta fue correctamente construida no hay necesidad de confirmar con los datos crudos. Luego vamos tachando de extremo a extremo hasta que nos quede un solo valor. Si quedan dos valores, sumamos y dividimos el resultado entre 2.
Que más puedo decirte...? Te diré como le dijeron a un varón con un gran desafío por delante:
Mira que te mando que te esfuerces y seas valiente; no temas ni desmayes, porque Jehová tu Dios estará contigo.
Josue 1:9
En verdad este que tienes por delante no es taaaaan gran desafío como el de Josué, pero yo si creo que necesitas esforzarte... así que adelante..! Dios te guíe a un provechoso tiempo de estudio.
























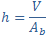





No hay comentarios:
Publicar un comentario